2020. 4. 10. 10:51ㆍ알고리즘/이론
목차
1. Dijkstra 알고리즘의 개념
2. Dijkstra 알고리즘의 구현
정의
Dijkstra 알고리즘은 방향 혹은 무방향 그래프에서 임의의 시작점으로부터 다른 모든 정점까지 최단거리를 구해주는 알고리즘 입니다.
Dijkstra 알고리즘을 사용하기 위해서는 한 가지 전제조건이 필요한데, 그래프의 어떠한 가중치도 음의 값을 포함하고 있으면 안됩니다.
개념
Dijkstra 알고리즘의 동작 방식에 대해 알아보겠습니다. Dijkstra 알고리즘을 수행하기에 앞서 임의의 시작점으로 하여금 자기 자신을 제외한 모든 정점까지의 거리를 무한대 값으로 초기화합니다.
1. 아직 방문하지 않은 정점들 중 거리가 가장 짧은 정점 하나를 선택하여 방문합니다.
2. 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신합니다.
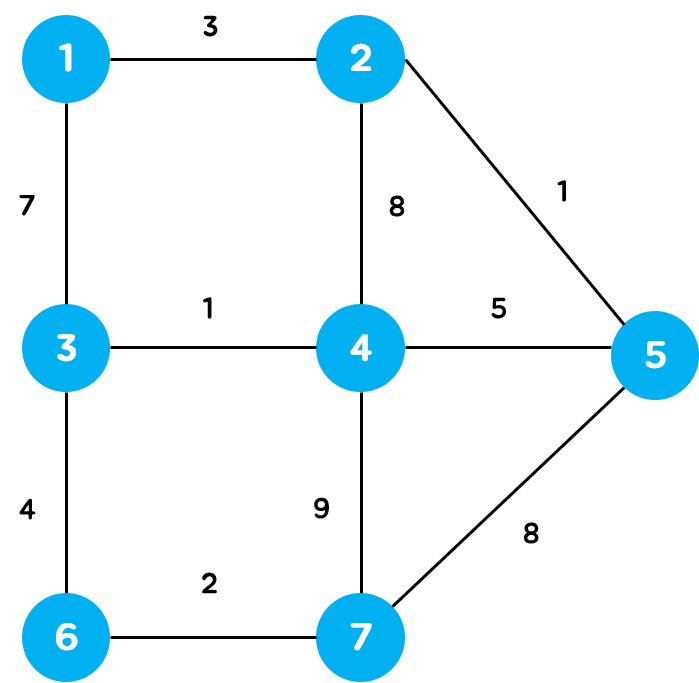
그래프를 통해 Dijkstra 알고리즘의 동작을 살펴보겠습니다.
dist[ ]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
다음과 같은 무방향 그래프가 있을 때 임의의 시작 정점을 1로 선택하여 Dijkstra 알고리즘을 수행하겠습니다.
먼저 시작 정점을 제외한 모든 정점간의 거리를 무한대로 초기화 합니다. 해당 데이터를 저장할 배열을 Distance의 약자로 dist[ ] 배열이라고 하겠습니다.

시작 정점 1에서 갈 수 있는 인접한 정점은 2와 3이고, 1번 정점을 통해 해당 정점으로 이동하는 거리는 아래와 같습니다.
- 2 : dist[1] + 3 = 0 + 3 = 3
- 3 : dist[1] + 7 = 0 + 7 = 7
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 3 | 7 | ∞ | ∞ | ∞ | ∞ |
만약 dist[2] > dist[1] + 3 이라면 dist[2] 는 dist[1] + 3 으로 갱신됩니다.
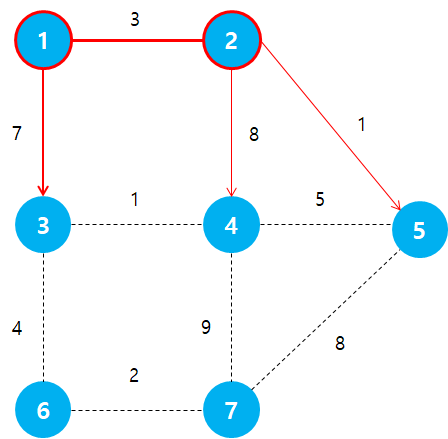
그 다음 아직 방문하지 않은 정점들 중 dist[ ] 가 가장 작은 정점이 2번 정점이므로 해당 정점을 방문하여 인접한 나머지 정점들에 대한 거리를 갱신합니다. 이 때 이미 방문한 정점 1에 대해서는 갱신이 이루어지지 않습니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 3 | 7 | 11 | 4 | ∞ | ∞ |
위와 같은 과정을 반복하면 아래의 그래프와 같이 정점 1에서 시작하여 각 정점까지의 최단 경로를 구성하는 그래프를 완성할 수 있습니다.

| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 3 | 7 | 8 | 4 | 11 | 12 |
코드를 통해 다음의 과정을 살펴보도록 합시다.
코드
// 정점의 개수 v, 간선의 개수 e, 시작 정점 k
static int v, e, k;
// 다익스트라를 위한 인접행렬 생성
static List<Edge>[] graph;
// 거리정보
static int[] dist;
// 간선을 정보를 관리하기 위한 객체 생성
static class Edge implements Comparable<Edge>{
int v, w;
public Edge(int v, int w) {
this.v = v;
this.w = w;
}
@Override
public int compareTo(Edge e) {
// TODO Auto-generated method stub
return this.w - e.w;
}
}
public static void main(String[] args) throws Exception {
// 거리 정보를 저장하기 위한 배열을 초기에 무한대로 초기화 합니다.
dist = new int[v+1];
Arrays.fill(dist, Integer.MAX_VALUE);
// 탐색을 위한 인접리스트를 생성합니다.
graph = new List[v+1];
for(int i = 1; i<=v; i++)
graph[i] = new ArrayList<>();
// 인접리스트를 구현합니다.
for(int i = 0; i<e; i++) {
...
graph[u].add(new Edge(v, w));
}
// 우선순위큐를 생성합니다. 초기 우선순위 큐에는 시작정점이 들어있고
// 시작정점의 거리정보를 0으로 초기화합니다.
PriorityQueue<Edge> pq = new PriorityQueue<>();
dist[k] = 0;
pq.add(new Edge(k, 0));
// 최단 경로를 찾는 탐색을 수행합니다.
while(!pq.isEmpty()) {
// 현재 간선 정보를 받아옵니다.
Edge edge = pq.poll();
// 연결된 정점과 해당 간선의 가중치
int curr = edge.v;
int cost = edge.w;
// 해당 정점이 인접리스트에 포함되어있는지 확인
if(dist[curr] != cost) continue;
// 그 정점으로부터 이동할 수 있는 간선들을 탐색합니다.
for(Edge e : graph[curr]) {
// 거리정보를 갱신합니다.
if(dist[e.v] > dist[curr] + e.w) {
dist[e.v] = dist[curr] + e.w;
pq.add(new Edge(e.v, dist[e.v]));
}
}
}
}
}
위의 코드에서는 가장 기본적인 형태의 Dijkstra 알고리즘의 동작을 구현하였습니다. 먼저 시작점으로부터 모든 거리 정보를 담을 dist[] 배열의 값을 무한대로 초기화합니다.
그 다음 우선순위 큐에 시작정점을 넣고 시작정점에서의 거리 정보를 0으로 초기화합니다. 반복을 수행하면서 현재 정점과 연결된 정점들의 거리 정보를 갱신하고 갱신된 간선정보를 다시 우선순위 큐에 넣고 반복을 수행합니다.
이 때 우선순위 큐에서 탐색을 수행할 간선인지 아닌지를 결정하는 것은 if(dist[curr] != cost) continue; 부분입니다.
현재 정점에서의 가중치 값과 거리 정보상의 거리값과 같지 않으면 현재 거리 보다 긴 거리 정보이므로 무시하고 다음 간선정보를 받아옵니다.
위의 Dijkstra 코드의 시간복잡도는 우선순위 큐의 시간복잡도인 O(log V)에 최대 간선의 횟수만큼 반복을 수행하므로 O(Elog V)가 됩니다.
하지만 위의 코드를 인접 리스트가 아닌 인접 행렬로 구현했다면 매번 인접한 정점을 찾아야 하는데 탐색할 때 마다 정점의 개수만큼의 시간이 필요하므로 총 V개의 정점이 있다면 O(V2) 의 시간복잡도가 소요될 것이고 알고리즘의 시간복잡도는 최종적으로 O(V2log V)가 될 것입니다.
'알고리즘 > 이론' 카테고리의 다른 글
| [알고리즘] 탐색(2) - 순열(Permutation) (0) | 2020.04.11 |
|---|---|
| [알고리즘] 탐색(1) - 완전탐색(Brute-force) (0) | 2020.04.10 |
| [알고리즘] 정렬(6) - 퀵 정렬(Quick Sort) (0) | 2020.04.10 |
| [알고리즘] 그래프(4) - 최소신장트리 MST (2) (0) | 2020.04.09 |
| [알고리즘] 정렬(5) - 병합 정렬(Merge Sort) (0) | 2020.04.09 |