2020. 4. 13. 22:18ㆍ알고리즘/이론
개념
가지치기(Pruning)는 탐색 과정에서 필요없는 과정을 줄여 최적화 시키는 것입니다. 단편적인 예를 들면, 탐색한 값들 중 최솟값을 구하는 문제에서 현재까지 탐색한 결과값보다 값이 커질 경우 더이상 탐색하지않고 종료하는 것이 가지치기입니다.
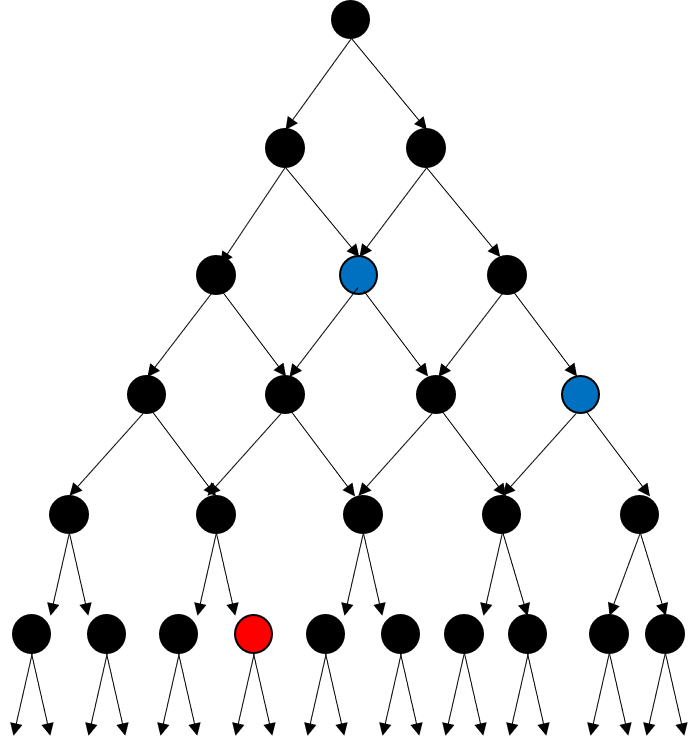
위 사진*은 특정 방법으로 노드 하나하나 탐색하고 있을때, 결과의 최솟값을 구해야하는 문제에서 모든 곳을 탐색한 경우의 수라고 가정해보겠습니다. 이 문제의 답이 빨간색 노드가 가지고있는 값이 최솟값이라고 하고 파란색 노드가 빨간색 노드의 값보다 커지는 위치라고 했을때, 위처럼 모든곳을 탐색할 필요가 있을까요?

파란색 노드 아래로는 탐색하지 않아도 적어도 최솟값이 아니란걸 알 수 있습니다. 따라서 탐색하지 않고 종료하는것이 가지치기 입니다.
* 설명을 위한 사진으로 탐색 순서가 논리적으로 맞지 않을 수 있습니다.
잠시 조합코드를 가져와 보겠습니다. 아래 코드는 n개의 원소중 r개를 뽑아 r개의 합이 최소가 되는 값을 구하는 코드입니다.
// nCr
void Combination(int idx, int curr, int n, int r)
{
if (idx == r)
{
result = min(result, sum);
return;
}
for (int i = curr; i < n; ++i)
{
sum += arr[i];
Combination(idx + 1, i + 1, n, r);
sum -= arr[i];
}
}
위 코드는 nCr을 모두 구해보고나서야 종료되겠죠. 그러나 우리가 위에서 배운 방법을 아래와 같은 코드 한줄을 함수 맨위에 넣어줌으로써 적용시킬 수 있습니다.
if (sum >= result) return;
가지치기는 이 한가지 사례에 국한되지않으며 문제에따라 적용할 수 있는 기법이 다릅니다. 때로는 그리디하게 접근을 해야할 수도있습니다.
또한 가지치기는 휴리스틱(heuristic)부터 DP(Dynamic Programming)에 사용되어지는 메모이제이션(Memoization)을 통해서도 더욱 최적화 시킬 수 있습니다. 그러나 이는 심화과정이고 이 포스트에서는 다루지 않습니다.
참조
구종만. 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 (Algorithmic Problem Solving Strategies). 인사이트. 2012
'알고리즘 > 이론' 카테고리의 다른 글
| [알고리즘] 정렬(7) : 위상정렬 (Topological Sorting) (0) | 2020.05.03 |
|---|---|
| [알고리즘] DP - 이항계수 (Binomial coefficient) (1) | 2020.04.23 |
| [알고리즘] 탐색(4) - 부분집합(Subset) (0) | 2020.04.12 |
| [알고리즘] 탐색(3) - 조합(Combination) (0) | 2020.04.11 |
| [알고리즘] 탐색(2) - 순열(Permutation) (0) | 2020.04.11 |