2020. 4. 23. 13:44ㆍ알고리즘/이론
목차
1. 이항계수의 정의
2. 이항계수 점화식
3. 파스칼의 삼각형
4. 이항계수 구현
정의
이항계수는 이항식을 이항정리로 전개했을 때 각 항의 계수를 나타냅니다. 이항식 $(x + y)^2$ 를 전개한 결과는 다음과 과 같습니다.
$(x + y)^2 = x^2 + 2xy + y^2$
이 때 위의 전개 식에서 각 항의 계수인 [1, 2, 1] 이 나타내는 것이 바로 이항계수 입니다.
이항계수는 조합을 통해 구할 수 있습니다. 이번 포스팅에서는 조합을 통해 이항계수를 구하는 점화식과 이 점화식을 통해서 재귀적으로 그리고 동적계획법으로 이항계수를 구하는 방법에 대하여 알아보도록 하겠습니다.
점화식
이항계수를 구하는 점화식에 대해 알아보도록 하겠습니다. $(x + y)^n$ 이라는 이항식이 주어졌을 때 이항식의 k번째 항의 이항계수는 다음과 같이 표현할 수 있습니다.
$_nC_k = \binom{n}{k} = \frac{n!}{k!(n-k)!}$ 이 때 k의 범위는 $0 \leq k \leq n$ 입니다.
이항계수를 구하는 위의 식은 다음과 같은 점화식이 성립합니다.
$_nC_k = \binom{n}{k} = \begin{cases} \binom{n-1}{k-1} + \binom{n-1}{k} & \quad 0 < k < n \\ 1 & \quad k = 0 \text{ or } k = n \end{cases} $
위의 점화식이 잘 성립하는지 다음의 예시를 통해 확인해 보도록 하겠습니다. 다음과 같이 원소가 { 1, 2, 3, 4 } 인 집합에서 3개를 뽑는 상황을 가정하겠습니다. 이를 식으로 표현하면 $_4C_3$ 으로 표현할 수 있습니다.
위의 상황에서 먼저 원소 1에 대한 선택 여부를 고려한다고 했을 때 다음과 같이 두가지 상황으로 나뉘어집니다.
- 원소 1를 선택 한 경우 : 나머지 3개 중에서 2개를 선택 $_3C_2$
- 원소 1을 선택하지 않은 경우 : 나머지 3개 중에서 3개를 선택 $_3C_3$
각각의 경우의 수를 더한 결과가 $_4C_3$ 의 모든 경우가 되므로
$_4C_3 = _3C_2 + _3C_3$ 으로 표현할 수 있고 위의 점화식이 잘 성립함을 알 수 있습니다.
한가지 더 고려할 것이 k의 범위입니다.
위의 식에서 $_{n-1}C_k$ 부분을 살펴보게 되면, k는 그대로이고 n은 작아지게 되기 때문에 k가 n보다 커질 가능성이 있습니다. 따라서 위의 점화식을 적용할 수 있는 k의 범위는 $0 < k < n$ 이 됩니다.
파스칼의 삼각형
이항계수를 구하는 또 다른 방법으로 파스칼의 삼각형이 있습니다. 파스칼의 삼각형은 아래의 그림과 같은 관계가 성립합니다.
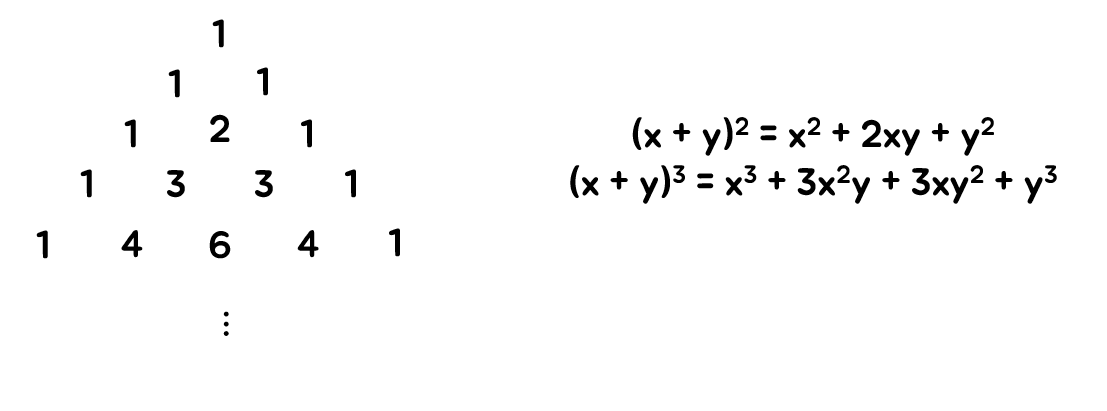
이 때도 이항계수의 점화식이 성립하는데 그 관계는 다음과 같습니다.

구현
그럼 이제 코드를 통해 이항계수 알고리즘을 살펴보겠습니다.
먼저 이항계수 알고리즘을 점화식 그대로 재귀로 구현할 수 있습니다.
static int bonomial(int n, int r) {
if(r == 0 || n == r)
return 1;
return binomial(n - 1, r - 1) + binomial(n - 1, r);
}하지만 이 경우에 n이 커질 수록 $_nC_k$의 값이 기하급수적으로 커지게 되는데 $O(n!)$ 의 시간복잡도의 재귀를 통한 구현방법은 큰 n 값에 대해서 결과를 구하려면 제한시간 내에 문제를 해결할 수 없을 것입니다.
두 번째 방법은 동적 계획법을 이용한 방법입니다.
static int[][] dp;
static int binomial(int n, int r) {
if(r == 0 || n == r)
return 1;
if(dp[n][r] == 0)
dp[n][r] = binomial(n - 1, r - 1) + binomial(n - 1, r);
return dp[n][r];
}
static int binomial(int n, int r) {
for(int i = 0; i<n; i++) {
// 0 ~ i 또는 0 ~ k 까지 중 작은 것을 택함 불필요한 것을 구하지 않기 위해서
for(int j = 0; j<=Math.min(i, r); j++) {
if(j == 0 || j == i)
dp[i][j] = 1;
else
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}
}
return dp[n][r];
}
}파스칼의 삼각형에서 알 수 있듯이 이항계수를 구하는 알고리즘은 중복 부분문제와 최적 부분구조를 만족하므로 동적 계획법을 통해 문제를 해결할 수 있습니다.
위의 코드에서 dp 라는 배열을 선언하여 각 단계에서 구한 이항계수의 값을 저장해 놓고 다음 이항계수를 구할 때 사용하고 있습니다.
동적 계획법으로 이항계수 알고리즘을 구현한 경우 아래의 반복문을 이용한 동적 계획법의 구현처럼 $O(n^2)$ 의 시간복잡도로 문제를 해결 할 수 있음을 알 수 있습니다.
'알고리즘 > 이론' 카테고리의 다른 글
| [알고리즘] 정렬(7) : 위상정렬 (Topological Sorting) (0) | 2020.05.03 |
|---|---|
| [알고리즘] 탐색(5) - 가지치기(Pruning) (0) | 2020.04.13 |
| [알고리즘] 탐색(4) - 부분집합(Subset) (0) | 2020.04.12 |
| [알고리즘] 탐색(3) - 조합(Combination) (0) | 2020.04.11 |
| [알고리즘] 탐색(2) - 순열(Permutation) (0) | 2020.04.11 |